ACOUSTICAL INFORMATION
▶︎SUMMARY
In general, the wider a string is displaced, the louder the resulting sound. This is because wider string displacement causes larger movements at the bridge, and the cello body. The more pressure with which a string is displaced, the tighter the angles into which the string bends during vibration and, as a consequence, the more overtones can take part in the vibration, thus overtone content increases. For the plucked and struck string, string displacement is equal to excitation force. The bowed string is more complicated: bow speed is equivalent to string displacement and bow pressure to excitation force. However, since bow speed and pressure are interdependent, and since increased overtone content has a strong psychoacoustic influence on loudness, this relationship is by no means clear-cut.
The case of the struck string is particularly complicated because of the relationship between striking force and impact duration, and the psychoacoustic effect of damping.
For very low bow pressures, there is insufficient energy to sustain the lower partials. In addition, the shape of the vibrating string is not bent in sharp enough curves to allow high partials to sound. The result is a mid-partial dominated timbre, flautando.
For very high pressures, the sound becomes distorted. The tension of the string might be increased, which is heard as a sharpening in pitch. For the bowed string, several departures from the normal vibration pattern are possible, depending on the relationship between bow speed and pressure.
▶︎DETAIL
Excitation Force
String displacement is the distance by which a string is moved (pulled by a plectrum, struck by a hammer or drawn by a bow) from its resting position. Excitation force is the energy with which the string is displaced.
If the string is plucked or struck, string displacement is equivalent to excitation force; the amount by which a string is pulled by a plectrum/moved by a hammer is necessarily equivalent to the energy of the pluck/strike. In the case of the bowed string, bow speed is the displacement force since it controls the width of the string’s lateral movement. Bow pressure is the excitation force, the perpendicular force (towards the cello body) that the bow exerts on the string.
String displacement causes a rocking motion at the bridge which incites vibration of the cello body. Large displacements incite large movements at the bridge and body; therefore, amplitude is proportional to string displacement. In other words, amplitude is proportional to plucking/striking force and bow speed.
Excitation force decides the shape of the kink in the vibrating string. High excitation forces shape the corner of the kink into sharper angles, allowing the string to vibrate in smaller sections, which facilitates the inclusion of higher partials. Lowering excitation force decreases tension, softens the angles of the vibrating string and gradually excludes higher partials. Therefore, overtone content is proportional to excitation force, which is: ‘amount of displacement’ in the plucked and struck string and ‘bow pressure’ in the bowed string.
In fact, separating bow pressure and bow speed as respectively controlling amplitude and overtone content is not as simple as this theoretical model suggests. Some psychoacoustic effects counteract this, the most significant of these being that increases in bow pressure, in increasing the ‘brightness’ of a tone, also increase its perceived loudness. The ear’s receptiveness to a certain pitch band explains this psychoacoustic effect. The fundamentals of cello tones in the common playing range are usually well below the band to which humans are most sensitive. However, the mid-range partials of these fundamentals are within this band. If their amplitudes are increased by increased bow pressure, a disproportionately significant increase in loudness is perceived by the ear.
Minimum and maximum excitation force
The general rules above operate within limits of maximum and minimum plucking, striking and bowing forces, between which a ‘normal’ sound is produced. The value of these limits is not fixed, nor is the distance between them. The limits change according to: contact point, vibrating string length, string thickness and, in the case of the bowed string, the relationship between bow speed and bow pressure.
The minimum excitation force is defined as the minimal value required for ‘normal’ sound, i.e., when it is high, larger excitation forces are required to produce a ‘normal’ tone and ‘underpressure’ effects (flautando, flautato) are more readily produced; and when it is low, the tone is stable under low excitation forces and very low forces are required to produce ‘underpressure’ effects.
The maximum excitation force is defined as the maximal value under which a ‘normal’ sound can be produced. When it is high, the string can sustain ‘normal’ sound under high excitation forces and ‘overpressure’ effects require very high excitation forces. When it is low, the string is less able to sustain high excitation forces and ‘overpressure’ effects are more readily produced.
The minimal and maximal excitation forces:
- – Increase as the contact point moves from the middle of the string towards the bridge or nut/stopping finger
- – Increase as string width increases relative to length (that is as a string is made shorter by stopping or, for a fixed stopping position, moving from a thinner, higher string to a thicker, lower string)
- – In the particular case of the bowed string, increase with bow speed.
For example, if the bow stroke is fast and/or close to the bridge/nut/stopping finger, low pressures are not sustainable (the overtone-takeover effect begins) and higher than ‘normal’ pressures are possible.
Furthermore, increases and decreases in minimal and maximal excitation forces occur at different rates; the difference between them is not constant. The limits of maximal and minimal string displacement are narrower at the bridge/nut/stopping finger and become broader at the mid point of the string. In other words, there is more scope for varying excitation force within ‘normal’ sound near the middle of the string and progressively less as the contact point moves towards the bridge/nut/stopping finger.
▷OVERPRESSURE AND UNDERPRESSURE EFFECTS
Various effects are possible beyond the limits of minimal and maximal excitation force:
Underpressure
Below minimal excitation force, the mid-range overtones dominate the timbre. Again, this is a special case of overtone-takeover; the fundamental is excluded from the sound and, in addition, the reduced excitation force weakens higher partials. In other words, timbre is ‘filtered’ at both ends, the tone is dominated by the mid-range overtones. The overtone most present in the sound depends on contact point and excitation force. The reason for this is as follows. Each overtone requires a minimum excitation force at a particular contact point in order to sound. This value increases as the contact point moves towards the bridge/nut/stopping finger. Contact point is relative to the wavelength of a particular overtone, for example, contact point is measured as ‘1/10 of a wavelength from the bridge’ not ‘3 cm from the bridge’. A fixed point on the string is always, relative to wavelength, closer to the bridge for the first overtone than the fundamental. Similarly, a fixed contact point is relatively closer to the bridge for the second overtone than the first, etc. Therefore, at a fixed contact point, minimal excitation force becomes increasingly lower for ascending partials. If excitation force is reduced, the string is not supplied with enough energy to sustain each successive overtone; one-by-one the fundamental and then the first, second, third… overtones ‘drop out’ of the sound. It is difficult for the cellist to control which overtone dominates the sound, but a progressive increase in order from the lower overtones is possible by gradually reducing excitation force.
Overpressure
Very high excitation forces increase the tension of the string. At first this restricts overtone content and then it begins to force the pitch of the string upwards. The string is relatively unstable under these conditions, producing pitch fluctuations and ‘noisy’ distortion sounds. A downward glissando is heard as the elasticity of the string returns it to its original tension as the sound decays. For the bowed string, high pressure causes a downward pitch bend. The exact reason for this is unclear. It could be that high bow pressure restricts the movement of the kink of vibration in the string, occasionally preventing it from passing the bow and causing fewer cycles of vibration between bridge and finger/nut than normal, i.e., resulting in a lower frequency.
▷A NOTE ON BOWING
Overpressure effects
More effects are possible on the bowed than the plucked or struck string at high excitation forces because of the relationship between bow speed and pressure, and the sustained nature of the technique:
Distorted noise
The roughness of tone associated with high excitation force occurs when the bow is unable to grip the string to incite regular vibration, i.e., when the relationship between bow speed and pressure is ‘wrong’, just above the maximum pressure associated with ‘normal’ vibration for a particular speed. Torsion and longitudinal vibration are often present under these conditions. The former encourages the ‘noisiness’ of the tone as it restricts the string from being gripped by the bow. The latter is heard as high-pitched, irregular squeaks and is particularly present at high bow speeds.
Undertones
Under consistent high bow pressure and at speeds slightly lower than ‘normal’, undertones are produced. These are tones lower than the fundamental frequency of a vibrating string. There has been no conclusive study that explains the production of undertones but Mari Kimura, composer and violinist credited with discovering the effect, has undertaken some research in this area in the form of recordings, performers’ guides, notation and collaborative research with acousticians. Bibliography link Kimura et al.’s proposed explanation is as follows. If the bow exerts high downward pressure on the string, the kink of vibration in the string is unable to pass the bow in the usual way. If this restriction is controlled such that the kink passes the bow at a frequency that is lower than the ‘normal’ frequency but nonetheless regular, the pitch of the vibrating string is lowered. This effect is very difficult to control (more so on the longer cello strings than on the violin); it is more easily sustained with very regular, quite slow bow speeds on short, thick strings. Several undertones are producible on the violin: a semitone, 7th and minor 3rd below ‘normal’ pitch (and perhaps more, Neville Fletcher suggests that intervals of a third, seventh, octave, ninth, twelfth and possibly lower are possible on the violin). Bibliography link Fletcher and Rossing (1991) p.285. These pitches are rarely ‘in tune’ with the fundamental pitch and intonation varies with contact point: the pitch is sharpened as contact point moves towards the bridge. A high component is also present in the sound. This is possibly vibration between bow and bridge.
Nageln/clicking sounds
Bowed under very high bow pressure, the string produces resonant ‘clicking’ sounds. Similarly to above, there has been little research into the mechanics of this technique. However, a summary of the likely process is as follows: the bow force is such that the kink of displacement in the string is prevented from passing the bow altogether. Instead it is reflected at the bow back to the bridge. In addition, a second kink passes between the bow and the nut (or stopping finger), also unable to pass the bow. The string then vibrates in two systems simultaneously: from the bridge-edge of the bow to the bridge and nut-edge of bow to nut (or the stopping finger, in which case the corresponding pitch is inaudible since the vibration has no means of coupling with the body of the instrument). Pulling the string upwards with the left hand increases the pressure between string and bow, and can enable better control of the speed of the clicking components.
▷THE RELATIONSHIP BETWEEN BOW SPEED AND PRESSURE
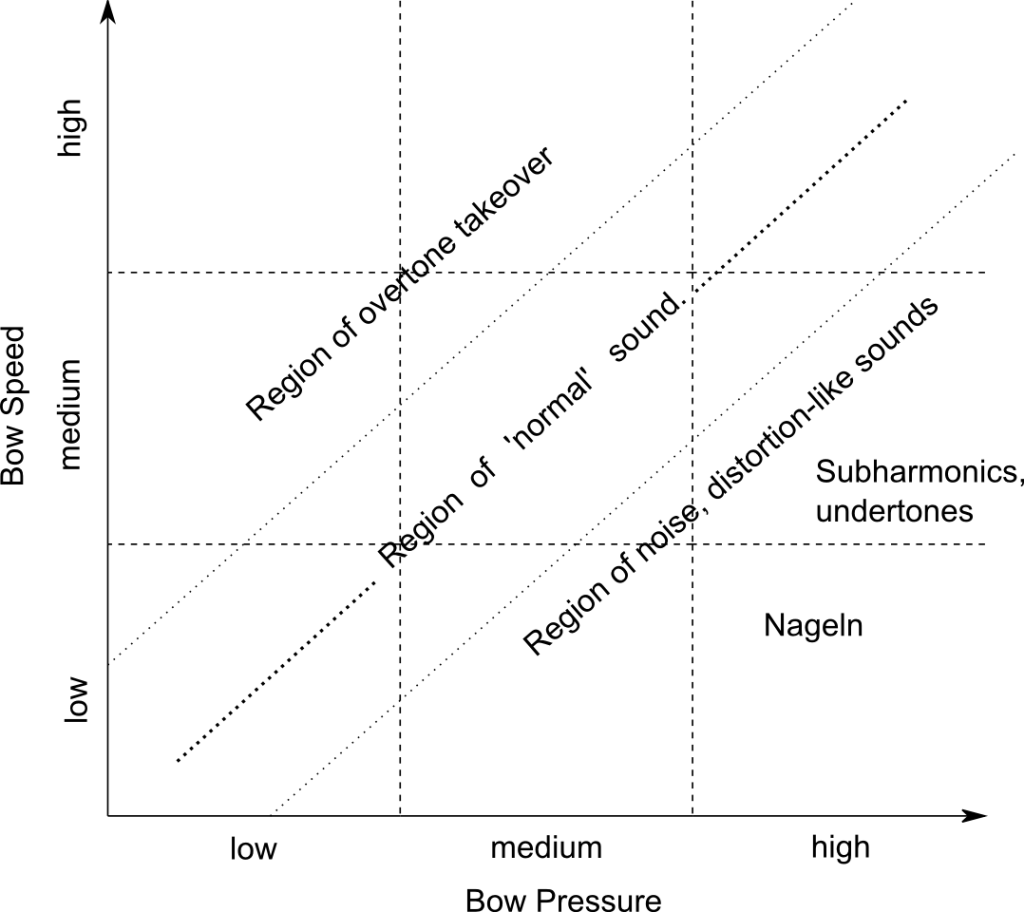
The interdependency of bow speed and bow pressure is inherently so well understood by cellists that ‘speed-pressure’ is almost perceived as a single force. To maintain a consistent rich/bright/full cello sound, certain adjustments in pressure need to be made for an increase in speed (or vice versa). These adjustments are so well practised that they are automatic to cellists. The overpressure techniques above require new technical coordination. The possibilities of speed and pressure combinations can be well represented on a speed-pressure vector. From the figure below it is clear that there is a band of speed and pressure variation within which ‘normal’ cello sound is produced, where speed and pressure are coordinated in the way well practised by cellists. At one edge of this band, the maximum bowing pressure for each particular speed, the sound becomes distorted and noise-based. At specific areas in this region, overpressure techniques are produced. It is clear that, since there is a continuous transition from the pressures and speeds required to produce noise-based sounds to those required to produce nageln and/or subharmonics/undertones, that a transition in sound also exists. This is heard as a mixture between noise and nageln and/or undertone pitches. At the other edge of the band of ‘normal’ sound, the minimum bow pressure for each particular speed, overtone takeover begins. The control of the dominance of specific partials in overtone takeover takes place at specific speeds and pressures in this region.
↩︎Plucking, Striking and Bowing the String: How? I-How far, How hard, How fast?
↪︎Plucking, Striking and Bowing the String:How III-Which direction?