*For a simple and efficient tool to help you find harmonics and multiphonics, download the new CELLO MAP APP
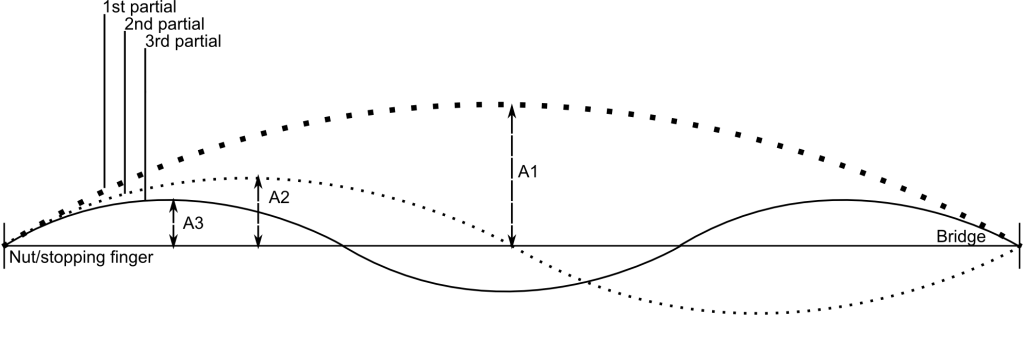
For a fixed excitation force and contact point, ascending harmonics become quieter. This is clear since at a particular excitation force, the deviation of the string from its rest position is greatest for the first partial and reduces with ascending partials. Amplitude depends on this deviation. The figure below shows a hypothetical situation where a particular excitation force displaces an ideal string. The total amplitude of the first partial is A1, which is greater than that of the second partial A2, which is greater than that of the third partial A3 etc. More precisely, the amplitude of the second partial is half that of the first, the amplitude of the third partial is a third of that of the first, etc.
▷IN CONTEXT
Controlling overtone content and loudness of harmonics
The reduced overtone content and reduced loudness of ascending harmonics mean that, while they broadly adhere to the principles of the effect of changing contact point, excitation force and means of excitation described in the case of the stopped string, the limits of these inputs are different (for fixed conditions, there are more possibilities for overtone-weak, quieter sound and fewer possibilities for high-overtone, loud sounds).
Moreover, since there can be multiple nodes on the string for the harmonic’s fundamental (this is a unique situation: the open/stopped string always has two nodal points at the nut/stopping finger/bridge), the ‘pattern’ of changing contact point is much more complicated in the case of higher harmonics than the stopped/open string. In reality, this means that a sul ponticello effect for harmonics is difficult to achieve: it will not contrast greatly with a sul tasto effect, and, since there are multiple nodal points on the string, there are also multiple points where sul ponticello and sul tasto might be found.
▶︎Note◀︎
Acoustical Information
The above figure only describes the situation for an ideal string. In reality, other factors influence the loudness of the partials. In fact, the struck string follows the above pattern most closely, with the amplitude of the partials decreasing by 1/n for ascending harmonic order. However, extra effects cause the equivalent equation for the plucked string to be (1/n)2 – in other words, the amplitude of the higher partials decreases more than the example above and more than in the struck string. For the bowed string, the equivalent formula is 1/n multiplied by a numerical constant (these formulas can be found in Author Benade’s The Fundamentals of Musical Acoustics (2nd edn., new York: Dover Pubications, 1990)). Therefore, the amplitude of the higher partials is much more reduced for the plucked string than the bowed string, which is more reduced than for the struck string. In fact the ‘clavichord-type’ battuto tones can negate this trend because of a masking effect. Applied to real circumstances, amplified by a cello body in a particular room, these results can diverge significantly from the above formulae. However, the pattern of amplitude reduction for partials can be heard loosely to follow the above description, and it is clear that the reduction of amplitude in the plucked string is greater than that in the bowed string.