ACOUSTICAL INFORMATION
▶︎SUMMARY
The overtone content of a sound changes for excitation points across the whole string length. Overtone content is weakest (sul tasto timbre) at the string’s mid point, or half-way between the stopping finger and the bridge. This is because there is a node at this point for all of the even-ordered overtones, and, being excited directly at a nodal point, a point of zero amplitude, these overtones do not sound. Therefore the potential overtone content is halved. Overtone content gradually increases (with some fluctuations) as the excitation point moves away from the mid point, towards the bridge or the nut/stopping finger, eventually being maximised close to the bridge or the nut/stopping finger (sul ponticello timbre). The change in overtone content is symmetrical around the string’s mid point. In fact, there is some differentiation from this general pattern in a real cello string and for tones bowed exactly at the mid point.
When excited very close to the bridge or nut/stopping finger, the fundamental and then the lower overtones drop out of the sound. This is because the excitation point is relatively too close to a node of these lower partials to sustain their vibration.
▶︎DETAIL
For any point of contact, the player will always ‘block’ or restrict a number of overtones. Depending on which/how many, this can have a significant influence on timbre. The acoustician, Arthur Benade refers to the overtones that contribute to a sound for particular playing conditions as the ‘vibration recipe’. Bibliography
In the plucked and struck string, overtone ‘blocking’ occurs because the process of excitation necessarily fixes the portion of string under the exciter (in contact with the plectrum or hammer) as an antinode, since it is exactly this portion that is being maximally displaced. Partials with antinodes at or close to the excitation point will contribute to the sound. However, partials with a node at the excitation point, where the ideal value is zero, will have reduced amplitudes or be excluded from the sound.
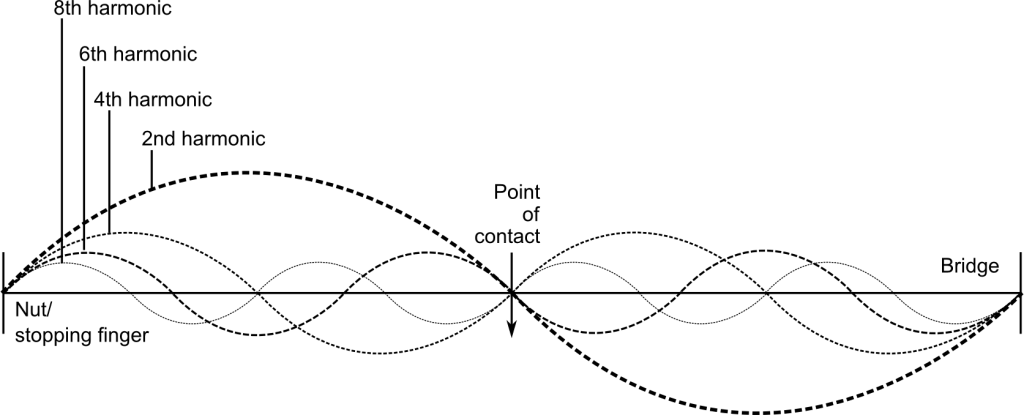
For example in the following figure, the plectrum/hammer displace the string at its mid point. This is ideal for the fundamental (first partial), which has an antinode at this point, and restrictive for the second partial, which would ideally have zero amplitude at this point.

Excitation at the above point affects more than just these two partials; in fact excitation at any point affects every partial by either enabling or restricting its vibration. The pattern of the timbral response to each excitation point changes significantly throughout the string length. Below are some examples:
If the point of contact is one fifth of the way along the string, the fifth partial is removed from the sound, as are the tenth, fifteenth, twentieth, twenty-fifth…5nth.
Since there are a finite number of partials in which a string can vibrate, a fifth of the string’s potential partials are excluded from the sound.
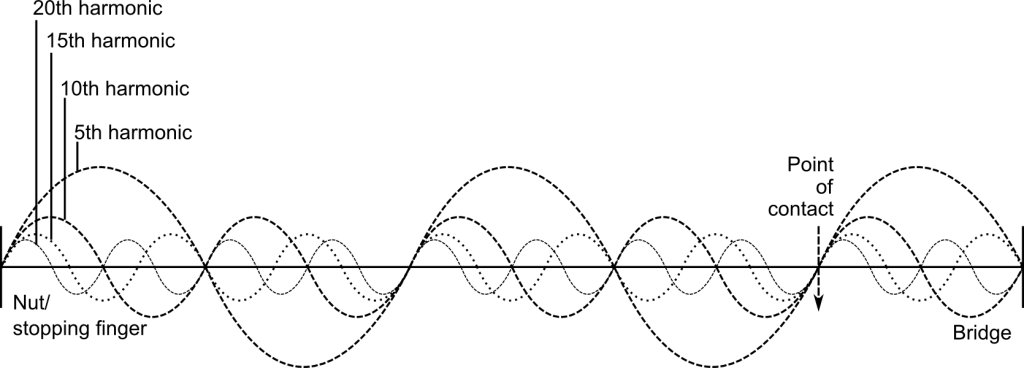
The number of higher partials in a tone is minimal when the point of excitation is at the middle of the vibrating length of string. The string vibrates with half of its potential overtone content, i.e., every other partial is excluded from vibration. This is the most extreme sul tasto timbre.
The second, fourth, sixth, eighth, tenth, twelfth…2nth partials are excluded from the timbre. Similarly, exciting a string at a quarter of its length removes a quarter of the potential overtones from the sound and at a third of its length removes a third of the string’s potential overtones from the sound, etc.
The situation in reality is less clear cut than the above examples suggest; sometimes extra partials are removed from vibration because of damping, string thickness, etc. and sometimes partials are re-added to the sound because of cello body responses, room acoustics, psychoacoustic effects, etc. However the above pattern is broadly perceivable as the contact point changes.
The situation for the bowed string is more complicated. Partials with nodes and antinodes at particular contact points are restricted by excitation since the bowing action, in constantly inputting energy into the system, both fixes the portion of string under the bow and forces it to move (consider the bowing mechanism: the string is ‘pulled’ at the speed of the bow and springs back to its rest position at a speed determined primarily by string stiffness). However, this process does not restrict partials with antinodes close to the bowing point. Consequently, the relationship between timbre and contact point is not significantly different from that of the plucked or struck string except that, as mentioned above, a string bowed at its mid point (either an antinode or a node for all partials) produces almost no sound.
In reality, many partials can have a significant involvement in cello sound, but to see the emerging of a general pattern I will consider a string that can only vibrate in partials 1- 13.
In the following figure, possible contact points on the string are shown alongside the number of partials excluded at that contact point:
For example, if the string is excited close to the nut, at the node for the thirteenth partial (contact point A on the diagram), one partial (the thirteenth) is excluded from the sound. As contact point moves towards the middle of the string, the timbre remains similar until the first node of the sixth partial (contact point B on the diagram), where two partials are excluded from the sound (the sixth and the twelfth). Moving towards the mid-point the spectrum becomes richer; only one partial is excluded (contact point C on the diagram). Approaching the mid point, the spectrum then changes as three, one, four (contact point D on the diagram), one, two, one and eventually six partials (contact point E on the diagram) are excluded respectively. The pattern is then mirrored in the upper half of the string (where ordinario playing normally takes place). In other words, on this very reduced model, there are areas of string close to the mid point that are as overtone-rich as those close to the nut/bridge.

▶︎▶︎NOTE
Research suggests that more than 40 partials contribute significantly to the sound of the open C string according to. See Gough (2007) p.560. Bibliography
Of course, the above diagram is a very over-simplified model for a cello string, where the number of overtones is higher (probably three or four times the above) and where other effects can influence sound significantly (for example, consider the possibility of covering more than one nodal point with the plectrum/hammer/bow). However, the general pattern of distribution is applicable and the following general points are true to both the model and the real cello string:
- – The contact point that excites minimal overtone content is at the mid point of the string.
- – As the contact point moves away from the mid point of the string, the overtone content of a sound increases nonlinearly with some fluctuations.
- – The pattern of variation in overtone content is symmetrical about the string’s mid point, i.e., a fixed distance from the bridge is equivalent in overtone content to the point the same distance from the nut/stopping finger.
- – There is a point near to the end of the string where overtone content increases at a faster rate without fluctuation (but still non-linearly).
When the contact point is very close to the extremities of the bridge or the nut/stopping finger, the fundamental is weak in relation to its overtones and the overtones dominate the timbre, ‘overtone takeover’. In this case, the excitation energy is inputted too close to a node of the fundamental to incite vibration. The partials drop out in ascending order (fundamental, second, third, fourth…) because contact point is relative to wavelength: any fixed contact point is closer to the bridge/nut/stopping finger in relative terms i.e., closer for the fundamental than the second harmonic, which is closer than the third harmonic, etc. Therefore, there is an excitation point close to the bridge at which the fundamental is excluded from the sound and the second partial dominates the timbre and, as this point moves further towards the bridge/nut/stopping finger, where the second partial can no longer be sustained and the third overtakes the timbre etc. The longer the string is and quieter the sound is (i.e., the lower the excitation force), the further from the bridge this effect takes place.
Point of contact is relative to string length: i.e., a fixed excitation point (e.g., 3 cm from the bridge) for stopped strings is relatively further from the bridge than for (longer) open strings. This implies:
- – To maintain a consistent tone when shifting with the left hand towards the bridge, the point of excitation must move correspondingly (this movement becomes natural to cellists).
In other words, this implies that the sul ponticello effect will be more extreme when a string stopped in first position is excited a centimetre from the bridge than when the same string, excited at the same point is stopped in fourth position. In addition to this: increased string width in relation to string length limits higher partials. This is because the string can only vibrate at partials with wavelength greater than string width. Some important implications of this are:
- – At any fixed stopping position, a progressively less extreme sul ponticello sound is producible on the (thicker) D, (even thicker) G or (thickest) C strings than on the A string.
- – For a fixed string length and a fixed point of excitation, the number of higher partials in a sound diminishes from A to D to G to C string.
↩︎Plucking, Striking and Bowing the String:Where? I- Which side of Stopping Finger?