ACOUSTICAL INFORMATION
▶︎SUMMARY
As exciter width increases, progressively more nodal points for particular partials are covered during excitation. Partials with nodal points covered by the exciter are blocked from the sound. Therefore, overtone content becomes weaker. The denser the exciter is, the more damping is reduced and the sharper the angles in which the string vibrates, increasing overtone content.
▶︎DETAIL
The relationship between exciter width/density and overtone content is simpler to understand for the plucked and struck string than the bowed string.
Since the portion of string under the plectrum/hammer is displaced by an equal amount during excitation, this portion of string is fixed as vibrating more or less in the same phase of a wavelength. If a particular partial has a node and an antinode within this band the partial will barely sound. The following diagram demonstrates this for the 20th partial:
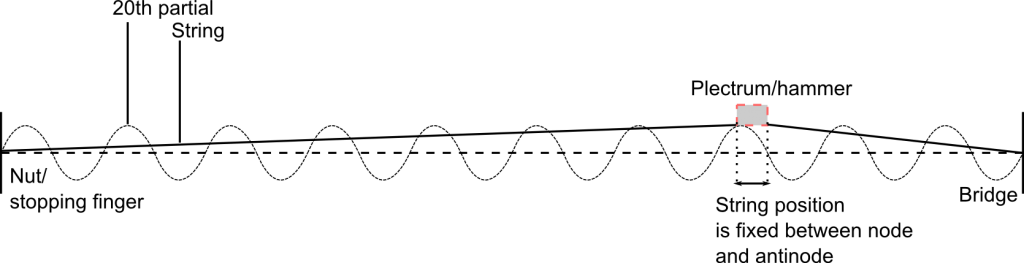
Such exciters with width ‘antinode-node’ have a variable influence on a partial’s response. In the above case, the partial is restricted but if the plectrum/hammer were shifted slightly to the left the partial would respond well. However, if the area of string covered by the exciter spans two points with opposing amplitudes for a particular partial, this partial will be excluded, or weakly present. Since two points with opposing amplitude always occur at exactly half a wavelength of a partial (except at a nodal point (0, 0) ), any exciter width equal to or above this excludes the associated partial. For example, in the figure below, the 20th partial will be blocked form the timbre.

Therefore, the exciter width sets the minimum wavelength of partials to be strongly present in the timbre and this value is twice the width of the exciter. The rate of the ‘dropping out’ of partials with increasing exciter width is higher for higher overtones, i.e., for a thin plectrum/hammer/bow, small increases in exciter width have a larger impact at first and then a progressively lesser impact for descending partials. This is clear because the difference between wavelengths of adjacent partials increases as the harmonic series descends. For very thin/very thick exciters, the overtone content is increased/decreased to the extent that point of contact becomes almost irrelevant to timbre. Theoretically, changes in bow width follow a similar pattern, although the different weights and lengths of wider/narrower bows e.g., violin, double bass, ½ size cello bows also affect sound.
A change in exciter width is, more broadly, a change in contact area between exciter and string. Several other factors equate to a change in contact area: If a soft hammer is used to strike the string, or if excitation force is low, the hammer material spreads out upon impact with the string, increasing the contact area between string and hammer. Dense hammers, or hammers struck with large excitation force, keep their shape on impact and the contact area is true to the width of the hammer, i.e., contact area is minimised. Similarly, the harder/further the plectrum pulls the string, the more tightly the string bends around it, reducing contact area. Therefore: perceived exciter width is inversely proportional to hammer density and the excitation force of the plectrum/hammer, so consequently these factors are proportional to overtone content.
In addition to this, exciter density has an impact on damping: using a dense hammer limits damping at the excitation point. The hammer absorbs less energy upon excitation. This favours higher partials. Therefore, hammer density is proportional to overtone content.
▷A NOTE ON PLUCKING
Plucking the string with more than one plectrum
Partials are either enhanced or restricted by two plectra exciting the string in the same or opposite directions. This depends on whether the plectrum is pulling the string into the shape of a particular waveform or against it. In both examples below, the partial (in this case the 10th partial) is enhanced because the placing of the plectra suits its waveform:
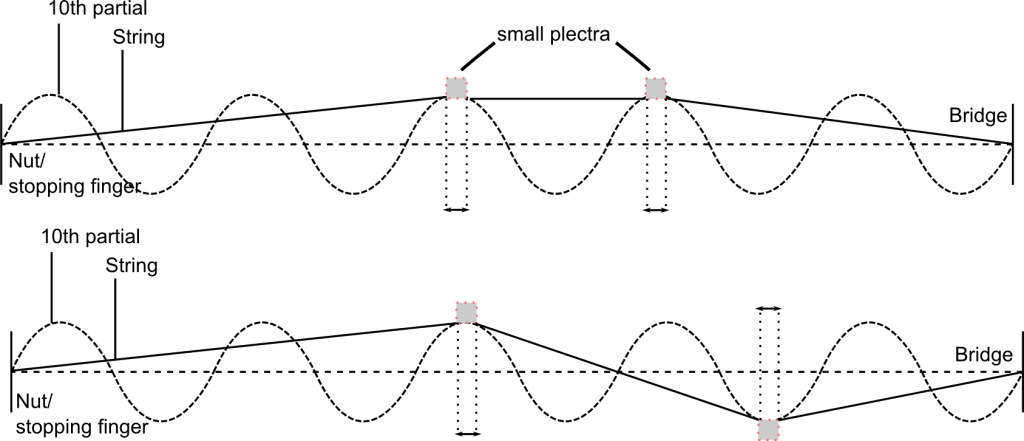
In both examples below, the partial (in this case the 10th partial) is restricted because the plectra are pulling the string against the shape of the waveform:
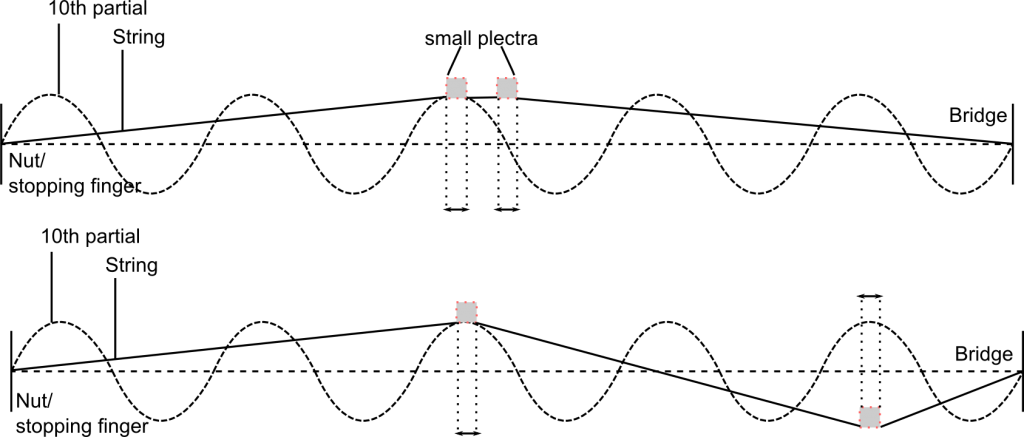
Since this reaction can be difficult to control, using more than one plectrum can have unpredictable results in timbral terms. However, a clear change in timbre and volume is heard between plectra at fixed positions exciting the string in the same direction compared with plectra exciting the string in opposite directions.
For example, consider a string plucked by two plectra at ¼ of its length and ¾ of its length, firstly with excitation forces in the same direction and secondly with opposing excitation forces. In the former case a strong contribution from the fundamental is heard and in the latter the fundamental is notably weakened and the second partial can be clearly heard in the sound:

▷A NOTE ON STRIKING
In the case of the hammered string, thin, dense hammers maximise the overtone content of piano-type vibration and wide, dense hammers maximise the overtone-content of clavichord-type. This is because as hammer width increases, so does the impact duration between hammer and string. During impact duration, the hammer is in contact with the string and applying a force in one direction. If a particular partial has a period equal to this duration then, by definition it requires the string shape to bend into opposite amplitudes within this time period. This is not possible because of the single force applied to the string; therefore the partial is excluded from the timbre. Moreover, even if partials have a period equal to half the impact duration they will only be weakly present in the timbre because the movement of the string is not flexible enough to suit their waveform. In fact, a particular partial only contributes strongly to piano-type vibration for impact durations less than half its period. Impact durations of between one and half the period of a particular partial may excite that partial weakly. Since period decreases with ascending partials, overtone content is inversely proportional to contact duration between string and hammer.
For clavichord-type vibration, the opposite is true: a partial only contributes if the contact time between hammer and string is greater than or equal to its period, i.e., a stable clavichord-type tone is only heard for impact times equal to one, or preferably more periods of the fundamental. This is clear since, as clavichord-type vibration takes place during the hammer’s contact with the string, at least one cycle of vibration must take place between hammer and bridge/nut for the fundamental to sound. Wide, soft hammers maximise duration, whilst soft hammers also have a damping effect; therefore wide, dense hammers produce the clearest clavichord-type tones. Controlling clavichord-type pitches by using hammer width and force to control impact time is not ideal. The damping effects that are associated with soft hammers and low excitation forces reduce the overtone content of the tone considerably, sometimes even restricting the fundamental. Striking with greater force and then holding a dense hammer to the string produces a much richer spectrum.